TUGAS
QUANTUM
COMPUTATION
“PERHITUNGAN ANALITIK ALGORITMA GROVER“
DISUSUN
OLEH :
RAHMA INDAH SAFITRI (55415553)
KELAS 4IA05
FAKULTAS TEKNOLOGI
INDUSTRI
TEKNIK INFORMATIKA
1.1
Latar Belakang
Perkembangan hardware komputer
pada saat ini telah ditunjukkan oleh meningkatnya jumlah microprocessor yang ada pada sebuah komputer. Demikian yang
ditunjukkan oleh Intel Corporation dalam https://www.intel.com/ pressroom/ kits/ events
/moores_law_40th /. Perkembangan software
juga ditunjukkan dengan
kemampuan komputasi sebuah komputer yang semakin cepat, meskipun komputer yang
ada sekarang masih beroperasi bersadarkan paradigma klasik atau serial,
sehingga sangatlah beralasan untuk mengembangkan sebuah komputer dengan
paradigma kuantum, hal ini dikarenakan ruang Hilbert yang digunakan oleh
mekanika kuantum sangatlah besar, sehingga beberapa permasalahan yang sulit
pada komputer klasik dapat diselesaikan. Selain itu salah satu fitur yang
ditawarkan oleh mekanika kuantum adalah prinsip superposisi yang memungkinkan
evaluasi dari semua keadaan dilakukan pada waktu yang bersamaan. Fitur ini juga
yang membuat komputer kuantum lebih powerfull.
Salah satu implementasi Quantum Computing sebagai sebuah model dalam paradigma komputasi yang
baru adalah algoritma pencarian database dengan menggunakan algoritma Grover.
Secara teori telah ditunjukkan bahwa pencarian dengan algoritma ini menunjukkan
hasil yang signifikan dalam pencarian data pada sebuah database, untuk itulah
pada penelitian ini bagaimanakan hasil dari simulasi dari algoritma tersebut terhadap
pencarian sebuah data pada database
1.2
Metode yang digunakan
Dalam artikel ini digunakan 2
metode yaitu dengan menggunakan Qubit dan Gerbang Kuantum. Berikut ini
penjelasan dari masing-masing metode
1. Qubit
Data
- data pada komputer direpresentasikan dalam bentuk bilangan biner yang disebut
bit, yang bernilai 0 atau 1. Pada
komputer klasik, kita dapat menuliskan sejumlah 2n kemungkinan
dari data - data tersebut. Sebagai ilustrasi, misalkan data 5 bit dapat ditulis
ke dalam 32 kemungkinan. Karena kinerja pada komputer klasik berjalan secara
serial, maka pada setiap waktu kita hanya akan mendapatkan satu dari sejumlah
kemungkinan yang ada. Sehingga, untuk semua kemungkinan, kita melakukan
sejumlah 2n kali
perhitungan. Berbeda dengan komputer klasik, pada komputer kuantum representasi
data dituliskan dalam bentuk state vektor
yang disebut qubit ( quantum bit).
Sebuah qubit dapat
berada pada keadaan (state).
ebuah qubit dapat berada pada keadaan (state)
|0i atau |1i,
akan tetapi dapat juga berada pada keadaan superposi-si
|Ψi =α|0i+β|1i
dengan α dan β merupakan bilangan kompleks. Superposisi
ini yang memungkinkan kita untuk menuliskan semua keadaan dalam satu kombinasi
linier. Superposisi ini juga yang memungkinkan kita untuk mengevaluasi semua
kemungkian dalam satu kali perhitugan. Pada ruang vektor (1) dapat ditulis
sehingga vektor basis |0i dan
|1i masing-masing
Sebuah qubit dapat direalisasikan dari polarisasi photon, mengarahkan spin inti yang berada pada medan
magnet uniform, atau dari dua keadaan (ground state dan eksitasi) dari sebuah elektron yang mengorbit
inti.
2.
Gerbang Kuantum
Sebuah gerbang
kuantum adalah analog dengan gerbang logika pada komputer klasik. Gerbang
kuantum adalah komponen dasar dari algoritma kuantum. Perbedaan dalam konteks
klasik dan kuantum adalah gerbang kuantum diimplementasikan secara uniter
seperti
UU† =I
Salah satu
gerbang kuantum yang sering digunakan adalah gerbang Hadamard
yang biasa
digunakan untuk membentuk superposisi dari dua keadaan seperti berikut
Komputasi Kuantum dapat
diimplementasikan berdasarkan serangkaian gerbang kuantum yang beroperasi
secara uniter. Dalam mekanika kuantum operasi uniter ini diperlukan agar
probabilitas sistem setelah operasi tidak beruba dan sifat ini digunakan
sebagai dasar operasi berkebalikan pada Komputasi Kuantum selain prinsip
superposisi yang menjadikan Komputasi Kuantum lebih powefull terhadap komputer
klasik. Salah satu contoh sukses besar Komputasi Kuantum adalah algoritma
Grover pada masalah pencarian data dari sejumlah entri tak terurut dari suatu
basis data dengan kompleksitas waktu . Pada makalah ini kami tinjau ulang
tentang algoritma Grover tersebut, dan dibuat aplikasi untuk mensimulasikan
algoritma ini dalam bahasa pemrograman Java. Bagian teori makalah ini adalah
tinjauan ulang mengenai algoritma Grover, bagian simulasi berisi tentang
simulasi dalam bahasa pemrograman Java, dan bagian hasil dan diskusi
menjelaskan hasil dari simulasi yang diperoleh.
1.3
Analisa
Pada pencarian sejumlah M data suatu basis
data sepanjang N = 2n entri data tak terurut, algoritma Grover terdiri
dari dua register. Register pertama merupakan superposisi semua kemungkinan
state vektor, sementara register kedua merupakan register yang mengkodekan
solusi. Secara sederhana, algoritma Grover dapat ditunjukkan sebagai berikut :
1. Siapkan
sistem dalam keadaan superposisi
2. Lakukan Operasi Perulangan untuk operasi:
a.
b.
3. Lakukan
pengukuran terhadap |Ψ00i
Perulangan akan
behenti jika |Ψ00i=|ξi,
jika tidak maka ulangi langkah 2.
Oracle O pada persamaan (9) didefinisikan sebagai
O ≡I−2|ξihξ|
yang berfungsi
mem-flip-kan state vektor kepada solusi. Sementara operator D pada persamaan didefinisikan seperti
D ≡2|ΨihΨ|−I
atau dapat ditulis dalam bentuk matrik
D
|0i =1|000i
0
0
0
Penerapan
gerbang Hadamard pada sistem memberikan hasil
|Ψi =H|000i
untuk j merupakan nilai pada bilangan biner sehingga
(16)
Sesuai langkah pada Algoritma Grover maka Oracle
yang kita gunakan adalah
O = 1 0 0 0
0 0
0 1 0 − 2 0 1 0
0 0 1 0 0 0
1 0 0
= 0 −1 0
0 0 1
Sehingga penerapan Oracle pada sistem memberikan
Setelah itu, kita kerjakan operator Difusi pada
keadaan sistem terakhir
(19)
Substitusi
(16) pada (19) maka memberikan hasil
4√ 2 j = 0 4
√ 2
Sampai di sini selesailah iterasi
pertama dengan amplitudo solusi adalah
 78.125
78.125
8 √2 j = 0 8 √2
dengan amplitudo solusi adalah 94.53125.
1.4
Tanggapan
Algoritma kuantum merupakan algoritma
yang dikembangkan berdasarkan paradigma mekanika kuantum. Algoritma Grover yang
merupakan salah satu algoritma tersebut, memberikan hasil yang signifikan dalam
suatu pencarian data. Selain perhitungan secara analitik sebagaimana
diilustrasikan di atas, perhitungan numerik juga memberikan hasil yang
signifikan sebagaimana pada uraian berikut:
Pada pencarian data
dengan indek |3i = 0 0 0 1 ) T pada
basis data dengan jumlah data N = 4, dengan hasil bahwa state vektor yang
dicari ditemukan paad iterasi ke 1. Hasil simulasi untuk jumlah data N = 4 sampai N = 4096 diberikan oleh
Tabel.1. Tabel 1. Hasil simulasi algoritma Grover.
DAFTAR PUSTAKA
http://jurnal.radenfatah.ac.id/index.php/jifp/article/view/2798/1901 diunduh pada tanggal 7 Juli
2019 pukul 19:00




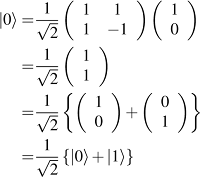





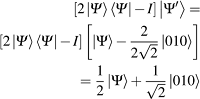
















0 komentar:
Posting Komentar